Failure Criteria for Prediction of Clinically Relevant Damage of Annulus Fibrosus
Narjes Momeni Shahraki, Ali Fatemi, Anand Agarwal and Vijay K Goel
DOI10.21767/2471-8173.100007
Narjes Momeni Shahraki1, Ali Fatemi1, Anand Agarwal2 and Vijay K Goel2,*
1Department of Mechanical, Industrial and Manufacturing Engineering Department, USA
2Engineering Center for Orthopaedic Research Excellence (E-CORE), Departments of Bioengineering and Orthpaedic Surgery, The University of Toledo, 2801 West Bancroft Street, Toledo, Ohio 3606, USA
- *Corresponding Author:
- Vijay K Goel
Distinguished University Professor, Endowed Chair and McMaster-Gardner Professor of Orthopaedic Bioengineering, Co-Director, Engineering Center for Orthopaedic Research Excellence (E- CORE)Departments of Bioengineering and Orthopaedic Surgery Colleges of Engineering and Medicine, University of Toledo, Toledo, OH 43606, USA
Tel: 41953080
Fax: 4195308076
Email: vijay.goel@utoledo.edu
Received date: September 25, 2015; Accepted date: November 24, 2015; Published date:November 28, 2015
Abstract
Internal disc damage (IDD) is a cause of chronic pain that 80 percent of people experience sometime during their life. It decreases quality of life and limits physical activities. Slightly degenerated discs in the lower lumbar intervertebral disc (IVD) are more susceptible to disc prolapse, associated with back pain.
Introduction
Internal disc damage (IDD) is a cause of chronic pain that 80 percent of people experience sometime during their life. It decreases quality of life and limits physical activities [1]. Slightly degenerated discs in the lower lumbar intervertebral disc (IVD) are more susceptible to disc prolapse, associated with back pain [2]. Formation of tears in the annulus fibrosus (AF) is recognized as the first sign of the disc degeneration process [3,4]. The tendency of the disc to herniate posteriorly and posterolaterally depends on many factors, including the loading conditions. Theoretical and experimental attempts have been made to address damage formation in the annulus. However, the relationship between initiation location and propagation of tears and loading conditions is not entirely explained.
With respect to the clinical studies and MRI images, there are three categories of annular tears in AF [5]: radial, circumferential (concentric), and rim (peripheral) lesions (Figure 1). Radial tears have been observed in the posterior and postero-lateral regions of the lower lumbar spine [6]. Concentric tears were distributed equally in the anterior and posterior regions [3]. Discrete peripheral tears or rim lesions [7] were seen more frequently in the anterior region at the junction of the endplate and disc [3,4]. The combination of these tears might also be seen in a disc, depending on the age, genetic background, and load history.
Physiological loading produces gradual prolapse. It starts with distortion in the lamellae of AF and forms fissures which cause protrusion of the nucleus polposus (NP) [8]. Experimental attempts involving human cadavers and animal models were made to investigate the relationship between annular tears and loading conditions [8]. Specimens were subjected to cyclic axial compressive loads ranging from 37 to 80 percent of their failure load limits and discs damage was reported in 2 of 11 specimens tested [9]. Vertebral or endplates damage were reported in the remaining 9 of 11 specimens [9]. In another study, cyclic compressive loads were applied to a motion segment with a predefined flexed position in which distortion of the posterior lateral area of the disc was observed [10]. Flexion-extension in addition to compression at three load levels of 260 N, 867 N, and 1472 N produced posterior and postero-lateral disc herniation [11]. Combination of flexion, axial rotation and compression produced annular tears and disc prolapse, which were peripheral at origin [12].
Conducting experiments to study damage initiation and progression are valuable to understand the injury mechanism of AF. However, it is difficult to identify the damage and its location and propagation under different and combined or multi-axial loading conditions. Moreover, these experiments may have error caused by uncontrolled variations of experimental conditions. Finite element (FE) approach is an effective tool which has been used for understanding spine kinematics in response different loading conditions [13-17]. Damage of the disc and stress distribution on the annulus fibrosus due to the different loads can also be studied using FE technique.
Damage and failure criteria are used in conjunction with FE analysis by several investigators. These criteria are based on strain, stress, or energy state within the AF. The maximum tensile strain criterion of the collagen fibers was used for failure analyses in AF under single and combined loads [18,19]. In another study intradiscal pressure in the nucleus, shear strain between annulus and adjacent endplates, and fiber strain in the annulus under combined loading scenarios were considered for predicting damage location [20]. The failure stress and strain data for soft tissues are quite inconsistent in the literature, depending on the strain rate used in performing the experiment. Three envelopes of yield and failure for collagen fibers were produced based on strain, stress, and strain energy density (SED) criteria using a nonlinear viscoelastic FE model of fibers [21]. The authors concluded that the critical value of stress did not change for a wide range of strain rates when SED criterion was used. However, ultimate stress and strain were different for a wide range of strain rates in various regions of the functional spinal unit. It was concluded that SED is a more practical failure criterion for AF region [21].
A disc model with stage (I) degeneration was used to explain delamination in the AF lamellae based on interlaminar shear stresses [22]. Maximum principal strain distribution in AF region was used to evaluate damage in a model based on hyperelastic anisotropic constitutive behaviour of AF [23]. Another study developed models of a healthy and a degenerated disc, to predict delamination using principal strain distribution [24]. In a recent study, damage initiation and progression in AF region under various cyclic loading conditions was studied using a 3D poroelastic FE model. The damage parameter used was the maximum principal tensile stress criterion in the annulus ground substance, along with linear damage accumulation for failure propagation [25]. Poro-elastic FE was developed to predict failure progression in a lumbar disc under heavy lifting cyclic loads [25]. The effects of fluid flow and strain dependent permeability were included in the analyses. Failure was defined when von Mises stress exceeded 2 MPa in the annulus matrix, 20 MPa in the nucleus and 4 MPa in the endplate [26].
Previously discussed studies either used a certain component of stress/strain such as fiber strain to quantify damage in the annulus under multi-axial stress/strain states, or combined different components of stress/strain in the form of von Mises distortion energy or principal stress/strain. However, these criteria have not been modified to account for the anisotropy observed in the AF material properties, especially its strength. Moreover, there is a limited knowledge about propagation of damage under combined loading conditions out of these studies. The Tsai-Wu criterion, a generalized form of von Mises distortion energy, has been used for anisotropic biomaterials such as tooth tissue [27] and vertebral trabecular bone [28]. Therefore, it is the goal of this work to apply and extend the use of this criterion to anisotropic soft tissues, such as AF.
Biaxial material properties of AF utilized in a hyperelastic anisotropic material model were shown to provide accurate results in terms of the biomechanical behaviour and stress distribution in the first part of this study [29]. Therefore, biaxial material properties of AF were used in present study. The aim of was to use two appropriate failure criteria for anisotropic materials, Tsai- Wu and maximum normal stress, to evaluate damage initiation and propagation under different loading conditions. Tsai-Wu failure criterion considers stresses and strengths of the material in different directions and results in a scalar value. Results from the Tsai-Wu criterion are then compared to maximum normal stress criterion to evaluate damage location and distribution in AF and its clinical relevance in predicting annular cracks.
Material and Methods
Finite element model
A previously validated 3D FE model of ligamentous functional spinal unit (L4-L5) [30] was modified for the analyses. The inferior surface of the L5 vertebra was rigidly fixed [29]. A hyperelastic anisotropic material model available in ABAQUS/StandardTM version 6.11 (Simulia, Inc., Providence, RI, USA) referred to as Holzapfel-Gasser-Ogden (HGO) [31,32] model, was used as the material model for AF. Biaxial material properties were used as material constants of AF for damage analyses. Properties of other elements of FE model such as bony elements, ligaments, and NP were kept the same as in the previous model [29]. Equation (1) shows the governing strain energy relation in the AF region:
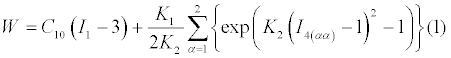
where C10, K1 and K2 are material parameters and the matrix is considered as incompressible material. Detailed description of this material model and values of constants for both uniaxial and biaxial conditions are reported in [29].
Strength properties in different directions
Strength varies as a function of direction in AF. Therefore, for conducting damage studies, stresses are compared to their respective strength limit of the annulus in the corresponding direction. Tensile experiments in the uniaxial state were performed in axial [33], circumferential [34], and radial [35] directions on multiple layers of AF lamellae and strengths of this tissue in these orientations were reported. Different anatomical regions of AF (posterior inner/outer and anterior inner/outer) represent different strengths and fracture strains in each direction as listed in Table 1. Mean experimental values of strengths in the axial and radial directions and mid-range value of circumferential direction were used in this study. Posterior and anterior regions were separated by a plane connecting the left and the right lateral regions. Three inner layers of AF close to the NP were considered as the inner region, and the remaining layers considered as the outer region, (Figure 2).
Table 1: Tensile strength and fracture strain in axial, circumferential and radial directions of the different regions of AF.
Literature on the compressive strength data of AF is very sparse. An experimental procedure was proposed [36] to study the mechanical response of this tissue to both initial and repeated compressive axial loads. Samples were prepared such that no continuous collagen fibers were coupled to the two endplates of the specimens, therefore, collagen fibers were not actively bearing load [36]. In the HGO material model used in this study, fibers cannot sustain compressive stress. Therefore, the compressive strength of AF was assumed as compressive strength of the ground substance from the experiments [36]. Annulus ground substance which is considered as an isotropic material [15-22], has the same strength in all directions. The compressive stressstrain curves up to failure of the annulus for different regions were obtained under monotonic and cyclic loading and similar failure compressive strengths for different regions of about 2 MPa were obtained under both types of loadings [36].
There are no published experimental results regarding the shear strength of AF. An analytical method was used to calculate shear strength from uniaxial tensile experiments on a single layer of AF [37]. Experiments were performed in longitudinal, transverse, radial, and circumferential directions. Based on Tsai-Hill failure theory for a symmetric composite, the shear strength was calculated to be 0.24 MPa. This value was used in the present study.
Failure criteria
Two commonly used criteria to evaluate damage under multiaxial stress states are maximum normal stress and distortion energy criteria. However, more general forms of these criteria are needed for anisotropic materials such as AF. These are described in this section.
Maximum normal stress criterion
There are three planes of principal stresses on which there is no shear stress. To find tensile strength of an anisotropic material in a particular direction (n), the following stress transformation is used:
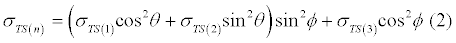
where, s are the material tensile strengths in three orthogonal directions. Axial, circumferential, and radial strengths of AF were considered as characteristic orientations (Figure 3a). Regional variation of the tensile strength in the anterior versus posterior and inner versus outer were considered based on the values listed in Table 1. Angles θ and ? specify the principal directions for each element, as illustrated in Figure 3b. Strength asymmetry of the material was considered and compressive strength in all directions was considered to be 2 MPa, as explained earlier.
To use maximum normal stress criterion the following steps were performed:
a. Stress components from FE simulations for each element of AF were used in a Matlab code to find principal stresses and directions for each element.
b. Tensile strength of the material was computed in principal directions using Equation (2).
c. Absolute values of maximum and minimum principal stresses were divided by the corresponding tensile or compressive strength of the material in the same principal direction. The maximum value of the two ratios for each element was considered as damage ratio. Damage distribution in AF for each specific loading condition was then obtained.
Tsai-wu criterion
The Tsai-Wu quadratic criterion can account for strength asymmetry and anisotropy, as well as interaction between strengths under multi-axial loading conditions. This failure criterion is a generalized form of von Mises criterion. The basic assumption of Tsai-Wu criterion is that there is a failure surface in the scalar form which can be found by the following equation [39]:

where Fi and Fij are the second and fourth rank strength tensors, respectively. The Tsai-Wu equation may be expanded and written in term of damage (d) for no failure, in the following form:

where s are normal stresses in three perpendicular directions and s are shear stresses. Stresses with respect to axial, circumferential, and radial directions for each element were used in this equation. The strength dependent F values in the equation were computed based on the assumed strengths accounting for the difference in tensile and compressive properties of different directions. Tensile properties for various anatomical regions of AF were considered, as listed in Table 1 and compressive strength was considered to be 2 MPa, as described earlier. Values of coefficients F’s and their corresponding equations are listed in Table 2. In this table, X, Y, and Z are tensile strengths in axial, circumferential, and radial directions, respectively, and X', Y', and Z' are the corresponding compressive strengths. Since compressive strength was assumed to be 2 MPa in all directions as previously discussed, X' = Y' = Z'. Also, Q, R, and S are shear strengths on circumferential-radial, axial-radial, and axial-circumferential planes, respectively, and Q', R', and S' are the corresponding shear strengths in the opposite direction. All of the shear strength values were considered to be 0.24 MPa, as discussed earlier. The contribution of shear stresses on axial-radial and circumferential-radial planes in the Tsai-Wu damage criterion is small, in comparison to axial-circumferential shear component. This is because of the small ratio of these stresses when divided by the corresponding shear strength of the material.
| Coefficients of Tsai-Wu Criterion [39] | AO | AI | PO | PI |
|---|---|---|---|---|
 |
0.09 | 0.61 | -0.24 | 0.61 |
 |
-0.25 | 0.33 | 0.3 | 0.41 |
 |
2.63 | |||
 |
0.29 | 0.56 | 0.13 | 0.56 |
 |
0.13 | 0.42 | 0.4 | 0.45 |
 |
1.56 | |||
  |
17.36 | |||
 |
-0.096 | -0.24 | -0.11 | -0.25 |
 |
-0.34 | -0.24 | -0.11 | -0.25 |
 |
-0.22 | -0.47 | -0.23 | -0.47 |
Table 2: Coefficients of Tsai-Wu criterion for different regions with their corresponding equations. Anterior outer (AO), anterior inner (AI), posterior outer (PO), and posterior inner (PI).
To use the Tsai-Wu failure criterion for AF, the following steps were executed:
a. Stress components in axial, radial, and circumferential directions for each element were obtained for each load condition.
b. F values for different anatomical regions of AF were calculated.
c.Damage values based on Equation (4) was calculated for different loading conditions and damage distributions in AF were obtained.
Analyses were done for different transverse surfaces in the height direction (inferior, superior, and mid-height). These surfaces were chosen based on the available planes with experimental results or the plane where maximum damage occurred.
Loading Conditions
It has been shown that follower loads can model compression due to muscle forces in the human spine, similar to the physiological conditions [40]. Therefore, all the compressive forces were simulated using follower loads concept in this study. Bending moments were applied to a reference point which was connected to all of the nodes of the superior surface of L4 by kinematic coupling. To assess damage location, various simple and combined loading conditions were applied to the functional spinal unit FE model (FSU), as listed in Table 3. Simple loads included compression, extension, or flexion. Combined loads included combination of compression with flexion or extension.
| Loading Case | Loading Condition | Damage Initiation Location Based on Tsai-Wu Criterion | Damage Initiation Location Based on Maximum Normal Stress Criterion | Experimental Results | Literature FEA Results |
|---|---|---|---|---|---|
| 1 | Pure compression (500 N) |
-Inferior surface -Posterior inner |
- Inferior surface -Anterior outer |
- Damage in the FSU was mostly at the end plates or vertebrae [44] - Posterolateral region [59] | -Posterior inner of inferior face [45] - Maximum von-Mises stress was at the outermost posterior close to endplate [59] |
| 2 | Pure compression (4000 N) |
-Inferior surface -Posterior inner and outer, anterior outer |
-Inferior surface -Anterior outer and posterolateral middle |
||
| 3 | Pure flexion (7.5 N.m) |
-Inferior surface -Posterior outer |
-Inferior surface -Posterior outer |
- Posterior outer inferior surface [45] - Maximum shear strain was at Posterior inner [20] - Maximum Tensile strain was at Postero-lateral outer [20] |
|
| 4 | Pure extension (7.5 N.m) |
-Mid height surface -Anterior inner |
-Mid height surface -Anterior inner |
- Maximum shear strain was at middle layers in the posterior region [20] - Maximum tensile strain was at Anterolateral inner [20] |
|
| 5 | Compression (500 N) and flexion (7.5 N.m) |
-Inferior surface -Posterior lateral inner |
-Inferior surface -Posterior outer |
-Inferior surface in the posterior and posterior lateral inner [2] | - Posterior inner inferior face [45] |
| 6 | Compression (500 N) and extension (7.5 N.m) |
-Inferior surface -Posterior inner |
-Superior and inferior surfaces -Anterior outer |
||
| 7 | Compression (4000 N) and flexion (8°) |
-Inferior surface -Nearly entire AF, radial tears in posterolateral |
-Inferior surface -Anterior outer and posterolateral (radial tear) |
-Inferior surface -Posterior region [2] |
|
| 8 | Compression (1400 N) and natural flexion (7°) |
-Inferior surface -Posterior lateral inner |
-Inferior surface -Anterior and lateral outer |
-Posterior lateral [43] |
Table 3: Comparison of damage initiation location based on Tsai-Wu and maximum normal stress criteria and with available experimental and FE models from the literature under different loading conditions.
A compressive load of 500 N was considered for the analysis, as suggested for modelling physiological loading condition of the L3- L4 level segment during standing posture [41] (load case 1, (Table 3). A compressive load of 4000 N has produced complete disc failure during cyclic loading in experiments [10]. Therefore, this load level was also considered to study propagation of damage in AF (load case 2, Table 3). Pure flexion and pure extension within the physiological range of intact motion segment, corresponding to 7.5 N.m moment were also applied to the model (load cases 3 and 4, Table 3).
For the combined loading scenarios, a 500 N compressive load and 7.5 N.m bending moments in flexion and also in the extension were applied to simulate loading close to the normal physiological condition (load cases 5 and 6, Table 3). It has been noted that during lifting activities compressive load that is applied to the lumbar spine by back muscles can reach six to eight times the weight which is lifted [10]. Therefore, a 4000 N compression load was applied to a hyper-flexed motion (8° flexed) segment to model heavy lifting similar to the available experiment studies [2-10] (load case 7, Table 3). It has also been shown that human motion segments during actual flexion is oriented at the x-axis minus 30° (based on the terminology of Panjabi et al. [42]) [43]. This loading condition with a combination of 1400 N compression (moderate lifting) and 7° flexion in this orientation on the L4-L5 disc was also considered (load case 8, Table 3). Except for results of natural flexion loading condition which was not symmetric, other loading conditions were symmetric with respect to the mid sagittal plane and, therefore, half of the disc is shown in the figures.
In another scenario, combination of 500 N compression load and 7.5 N.m flexion moment (5° rotation) in one model and 500 N compression load and 7.5 N.m extension moment (2° rotation) in another model were considered as initial conditions. Then in both models first the magnitude of compression force was increased to 2000 N (this is considered to be a high level of compression force) and the increase in damage values were calculated and compared to the initial model. Second, the compression load was kept at 500 N and the magnitude of flexion or extension in initial models was increased to the level that produced 8° or 4° rotation (considered to be a high level of rotational angle [40]), respectively, and the increase in damage value were compared with the initial models.
Results
Damage distribution and initiation location
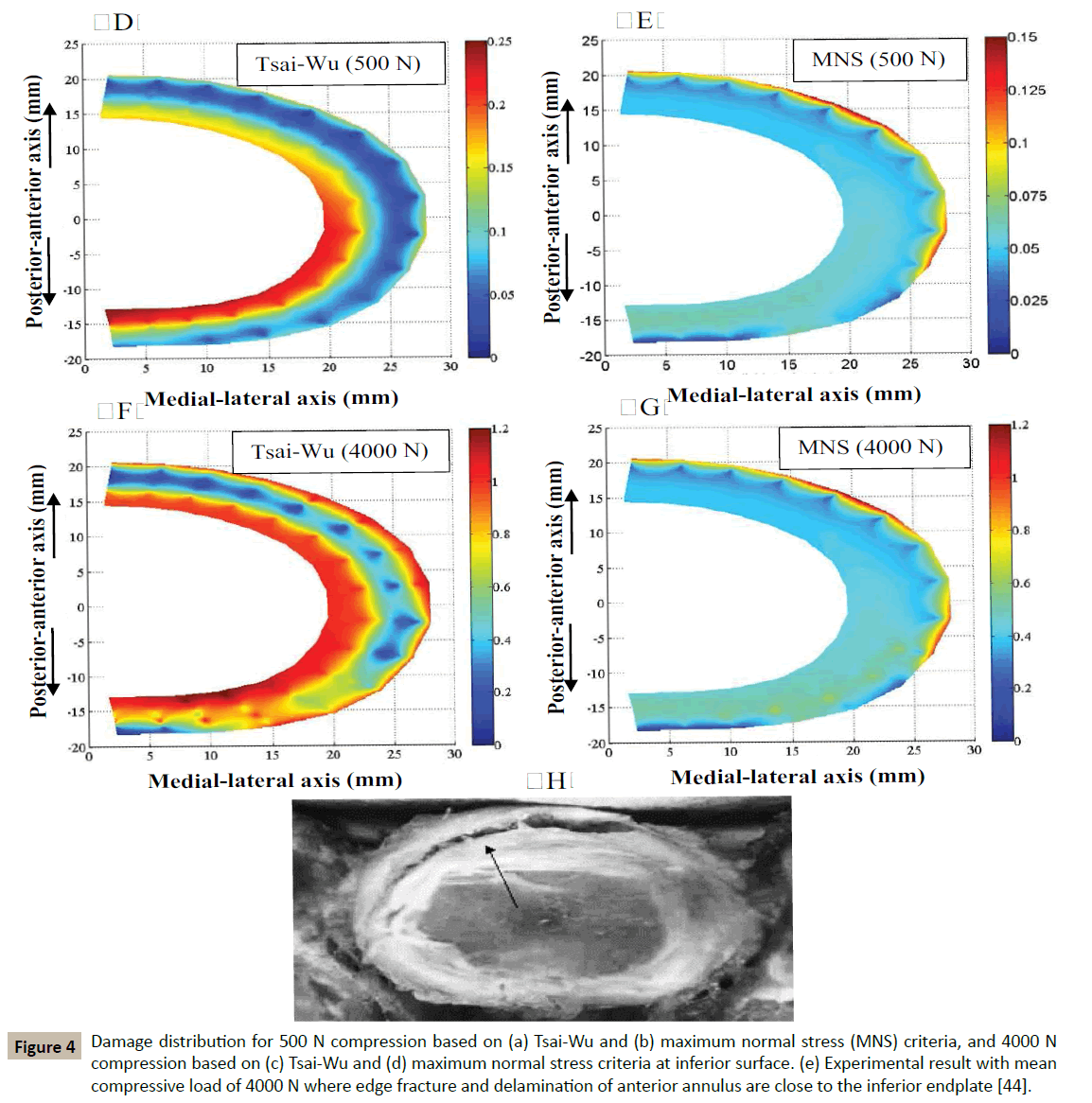
Based on the maximum normal stress criterion (MNS), under a compressive force of 500 N, damage initiates at the anterior outer region of the inferior surface (Figure 4b). Inferior surface was chosen to evaluate the results because available experiments for comparison are visible for this surface. Under a higher level of compressive force at 4000 N, damage propagates peripherally along the lateral region and extends radially to the next lamellae in the lateral site (Figure 4d). Circumferentially extended damage is observed in the postero-lateral region of AF under 4000 N compression. However, damage does not reach the innermost lamellae to form a radial fissure. Based on the Tsai-Wu criterion and under 500 N pure compression, initiation of damage is at the posterior inner region of AF and it propagates toward the lateral region (Figure 4a). By applying 4000 N compressive force, damage propagates in the outer region as well as at inner sites (Figure 4c). These two damaged regions connect in the posterolateral region and form a radial tear in the inferior surface.
Figure 4 Damage distribution for 500 N compression based on (a) Tsai-Wu and (b) maximum normal stress (MNS) criteria, and 4000 N compression based on (c) Tsai-Wu and (d) maximum normal stress criteria at inferior surface. (e) Experimental result with mean compressive load of 4000 N where edge fracture and delamination of anterior annulus are close to the inferior endplate [44].
Therefore, the two damage criteria predict different locations for initiation and propagation of damage under pure compression force. Based on both criteria, damage is relatively uniform in the thickness direction. Experimental results in Figure 4e indicate that under high compressive load of 4000 N failure occurs close to the anterior region, which matches well with predictions from MNS criterion in terms of initiation location. However, propagation of damage based on both criteria is in agreement with experimental results. MNS criterion predicts a lower damage value than Tsai- Wu criterion under 500 N compression. However, under 4000 N compression load, both criteria predict the same damage at the critical location.
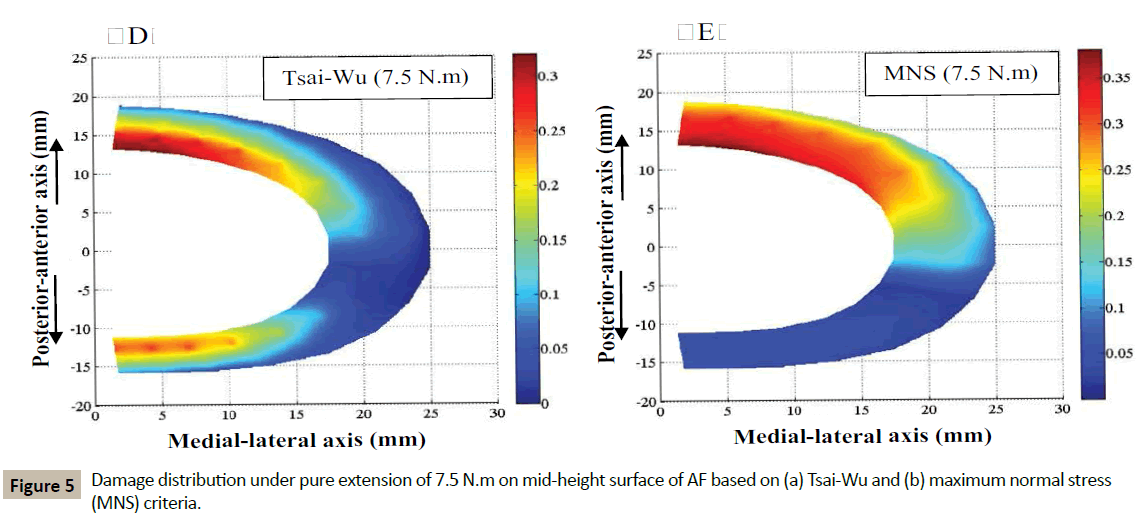
Under 7.5 N.m pure extension load, the maximum values of damage based on the MNS and Tsai-Wu criteria occur at the same location at the mid-height surface of AF. Damage distributions on this surface based on the two criteria are shown in Figure 5. MNS criterion predicts a slightly higher damage than the Tsai-Wu criterion under this loading condition.
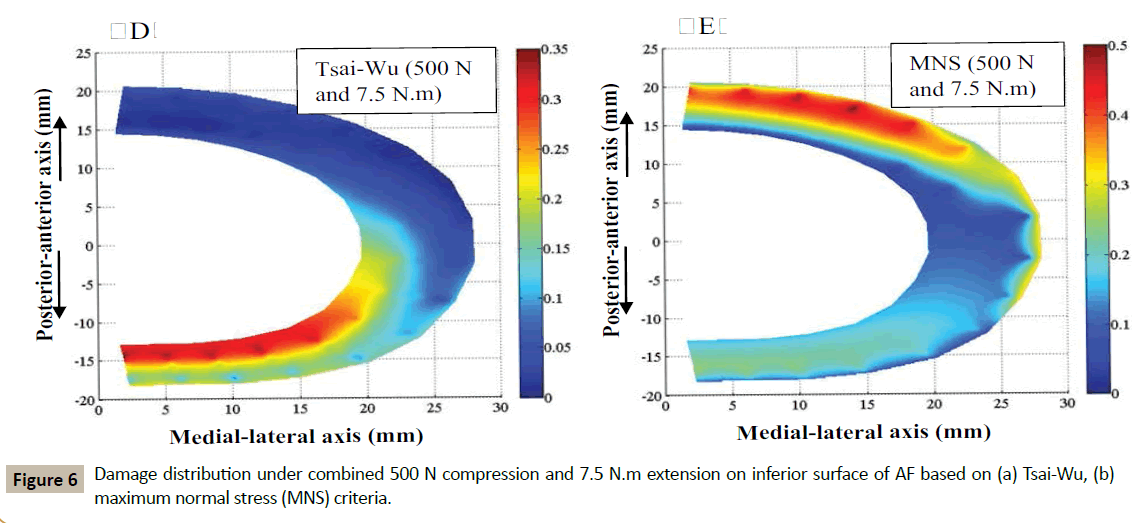
When extension is combined with compression, Tsai-Wu criterion predicts maximum damage in the inferior surface of AF, while MNS criterion predicts maximum damage at both superior and inferior surfaces. Damage distributions under 500 N compression and 7.5 N.m extension are shown in the same planes at inferior of AF in Figure 6. On this plane, Tsai-Wu criterion indicates that damage initiates at the first two layers of the posterior inner region. However, based on MNS criterion damage is located at the anterior region of the second and third layer. Therefore, damage initiation location, distribution, and propagation direction are different based on the two criteria. MNS criterion results in a higher degree of damage.
Under pure flexion of 7.5 N.m, the inferior surface had maximum damage values based on both damage criteria, shown in Figure 7. Damage initiated at posterior outer region of AF based on both criteria. However, Tsai-Wu criterion predicts extended damage in the circumferential direction, while MNS criterion indicates damage propagation in the radial direction. Therefore, the two criteria predict the same damage location, but different damage propagation under pure extension. Tsai-Wu criterion also predicts a higher degree of damage.
Under a combination of 500 N compression and flexion moment of 7.5 N.m and based on Tsai-Wu criterion, damage initiates in the inner part of postero-lateral region and extends circumferentially through the next layers towards the posterior region, (Figure 8a). MNS criterion predicts a higher damage at the posterior outer of the inferior surface of the annulus for this loading case, similar to the pure flexion case. MNS damage propagates both circumferentially and radially in the central region of the AF, (Figure 8b).
Figure 8 Damage distribution under combined 500 N compression and 7.5 N.m flexion based on (a) Tsai-Wu and (b) MNS criteria, and for combined 4000 N compression plus 8° flexion based on (c) Tsai-Wu and (d) MNS criteria on inferior surface of AF. (e) experimental nucleus extrusion from the posterior region of the disc close to the inferior surface under heavy compression and hyperflexion [2], (f) mid-height plane of the disc in the same loading condition [10].
Tsai-Wu criterion predicts radial tear in the postero-lateral region for 4000 N and 8° flexion angle in the inferior plane, (Figure 8c). For this loading, MNS damage occurs at the outer part of antero-lateral and postero-lateral region of AF peripherally and tends to form radial tears in the postero-lateral part of the annulus, (Figure 8d). Under this loading case, a larger area of AF experiences damage based on Tsai-Wu criterion, in comparison to MNS criterion. Failure of a specimen under a similar loading condition in an in-vitro experiment is shown in Figures 8e and 8f. Both experiments indicate damage at the posterior region of the disc and appearance of complete radial fissure is clear in both figures, which match the predictions for propagation of damage from both criteria. Although radial tears are predicted at high level of loading according to both criteria, the prediction of initiation locations of damage are different.
When the motion segment is subjected to 1400 N compression and 7° actual flexion angle, based on Tsai-Wu criterion the maximum damage is at the postero-lateral inner part of the annulus and close to the inferior surface, (Figure 9a). According to MNS criterion, however, the highest damage is at the anterior region of this surface, which propagates more peripherally and tends to form a rim tear, (Figure 9b). Damage distributions at the inferior surface of the annulus are compared with the available experimental result for a cut through specimen in Figure 9c. Since the damage distribution was similar in the height direction, inferior surfaces which have
The highest damage value are shown. As can be seen from this figure, Tsai-Wu prediction better matches with the experimental result. Therefore, the two criteria predict different damage initiation and propagation and MNS criterion predicts a higher degree of damage.
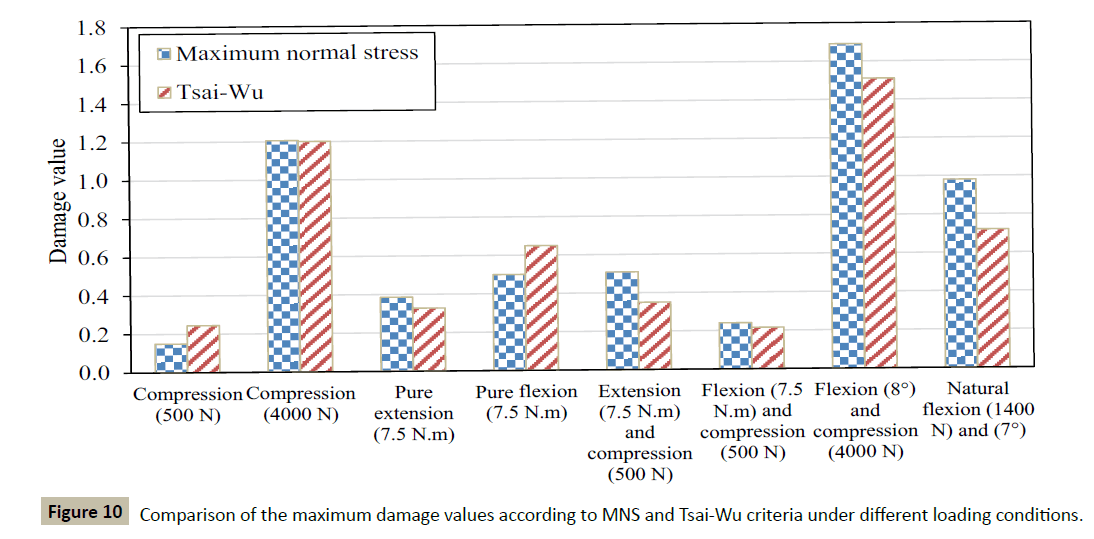
Comparison of loading cases and effect of increasing load
Figure 10 shows a comparison between maximum damage values based on MNS and Tsai-Wu criteria under different loading conditions considered. Based on this comparison, except for the 500 N compression load and 7.5 N.m pure flexion, MNS criterion predicts a higher or similar damage value at the critical locations. Under pure moments in flexion and extension directions, both damage criteria predict higher damage value for flexion which can be explained by the fact that posterior elements under extension tolerate some portion of the stress applied to the motion segment. Combination of flexion and compression at 7.5 N.m moment and 500 N load, based on either criteria decreases the maximum damage value compared to the pure flexion with 7.5 N.m moment.
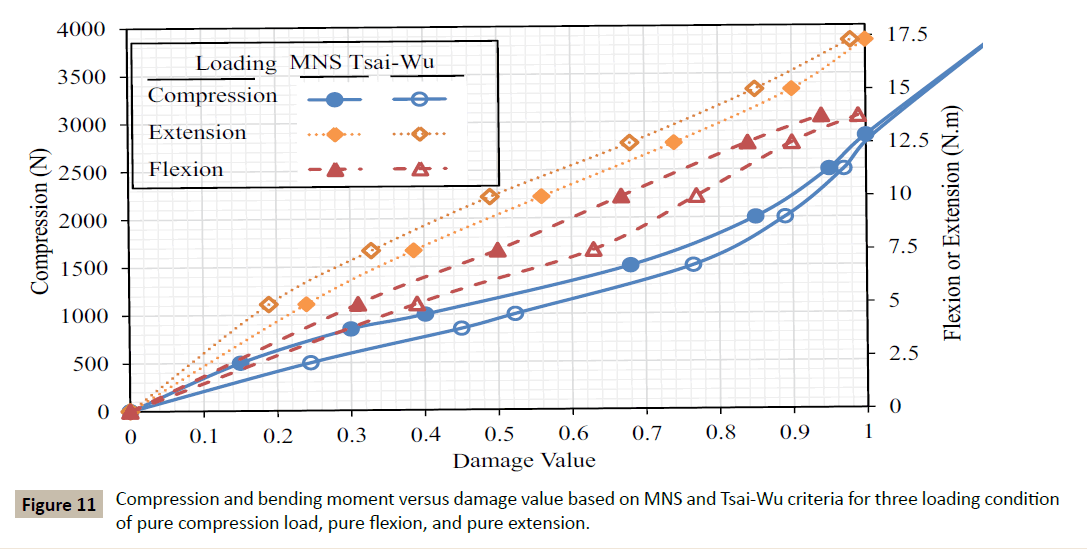
Increasing of damage due to increasing magnitude of pure compression load, pure flexion and extension moments on FSU based on the MNS and Tsai-Wu criteria is shown in Figure 11. This figure indicates that according to both criteria flexion produces a higher degree of damage than extension. However, this difference is larger for Tsai-Wu criterion. It can also be seen that while compression load damage increases nonlinearly with increasing load, for flexion and extension the trends are almost linear. Under pure compressive load, Tsai-Wu criterion predicts higher damage value than MNS criterion. However, with increasing the load level, damage values of the two criteria become closer.
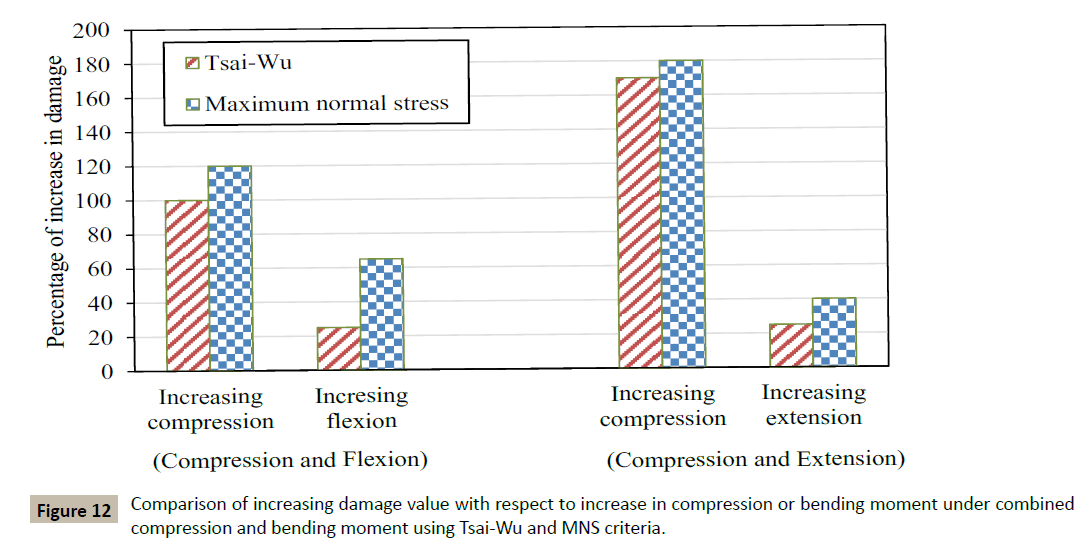
Effects of compression and bending moment (flexion or extension) in combined loading conditions (load cases 5 and 6) are shown in Figure 12. By increasing compressive force from the normal level of 500 N to a higher level of 2000 N in load cases 5 and 6, there is 100% and 170% increase in the Tsai-Wu damage values at critical locations, respectively (Figure 12). However, by increasing flexion and extension moments to a rotation of 8° and 4° in loading cases 5 and 6, respectively, increase in damage values are similar at 25% (Figure 12). Based on either criterion, it can be concluded that higher compressive forces produce more damage than higher bending moments. Also, increasing compression in extended FSU (load case 6) produces higher damage value than flexed FSU (load case 5) using either criteria.
Discussion
During different complex loading scenarios of spine various tissues can be at risk of injury. Damage in the disc can occur due to high level of loading or because of relatively low loads that are repeated many times. Herein, we investigated the risk of failure for different regions of annulus fibrosus under diverse static loading conditions to identify the location of damage initiation and its distribution by applying two damage criteria. Findings of this study correspond to and are validated by the damage location observed in experimental and clinical studies available in the literature.
During daily activities compressive forces, including body weight and muscle forces, are applied to the spine. These compressive loads increase to higher levels during lifting exertions. The pure compressive load of 500 N is a normal loading condition that is applied to the lumbar section in the standing position. A comparison of results from the current study by using Tsai- Wu criterion and other FE works under physiological level of compressive load indicates the same damage initiation location in the posterior inner region of AF [16-25,45-47]. At 4000 N compression both radial and rim lesions are predicted by Tsai- Wu criterion, while MNS criterion predicts only rim lesion. Experimental results indicate that under high magnitude of compression endplates damage and rim annular tears are more likely to occur in the intervertebral disc [44]. Degeneration and damage of disc due to low level of compression produces posterior and postero-lateral radial damage [7] as predicted by Tsai-Wu criterion.
In-vitro experiments show that when the spine is in a flexed position the nucleus moves posteriorly and when the spine is in the extended position it moves in the opposite direction [48], which can produce higher stresses in those regions. Based on both damage criteria, under pure flexion posterior region of the disc and under pure extension anterior regions were critical locations. However, disc failure is unlikely to occur by bending moment in the absence of compressive loads and under this loading condition mostly ligaments are at risk of failure [25] which was not the focus of this study. In addition, body weight is always applied to the spine motion segments in-vivo conditions. Under combined bending moments of 7.5 N.m and 500 N compression, critical location moves to the posterior and postero-lateral inner region of the annulus according to Tsai-Wu criterion, which also matches with other relevant FE results [25]. However, anterior outer and posterior outer damage locations under combined extension-compression and flexion-compression can be explained by clinically observed rim tears [7]. Based on this analysis, it can be concluded that during lifting objects it is better to keep a slightly flexed position. This can be explained by a lower intradiscal pressure during this posture than in upright position.
High compressive load such as 4000 N can be applied to a fully flexed motion segment, having 8° forward rotation while landing [49]. Damage analysis of this study by using both criteria predicted damage at the postero-lateral region of the inferior surface of AF in the form of radial tear, supported by in-vitro experiments [3] and clinical observations [50]. Based on the analyses, compressive force has the largest effect on the developing damage in AF. This situation happens mostly while lifting heavy items, which is one of the most common loading conditions leading to 50 to 75 percent of the low back pain [51]. Weight of an object is the most important factor for controlling damage during lifting.
Combination of flexion and compression is a common movement in real working life as documented by Fathallah et al. [52]. During these tasks, there is a coupled movement in the lateral direction [43], which was considered in this study by 30° orientation in the flexion direction with respect to the anterior-posterior axis. The initiation and propagation of herniation were studied using nucleus tracking in-vitro experiment [43], as shown in Figure 9c. These results indicate that herniation mostly initiated and propagated posterolaterally [2]. This is predicted by Tsai- Wu criterion for natural flexion combined with a moderate compressive load. Although MNS criterion for combined forward flexion and compression predicted clinically relevant results, its prediction was different from available experimental result [43] for natural flexion.
Table 3 represents a summary on damage initiation locations for different loading conditions and provides a comparison with other FE studies from the literature as well as with available experiments. According to this table different failure criteria result in different damage locations for some loadings cases, as expected. Most of the studies in the literature have concluded that damage occurs in the posterior and postero-lateral regions of the disc and there are limited studies on the progression of damage under combined loading conditions [20-25]. Since the stress state is multi-axial even in simple loading conditions due to the complex structure of AF, the results of this current study are important where all the stress components with respect to their corresponding strength are considered.
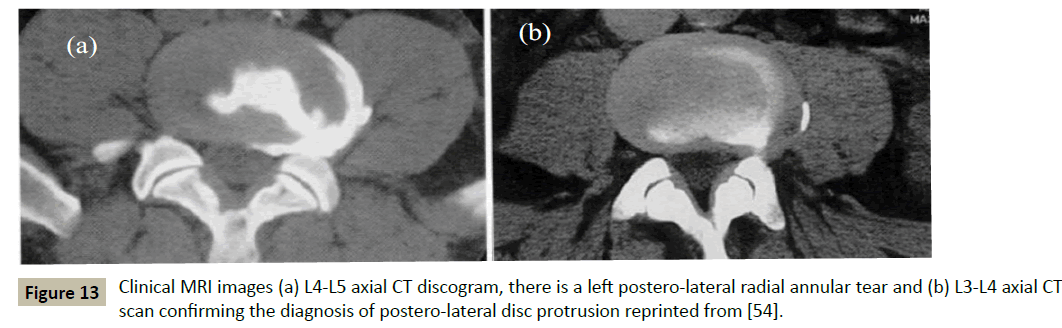
Based on the results of this study and according to Tsai-Wu damage criterion, except for extension, accumulation of damage is at the posterior region of the disc and close to the inferior endplate. High intensity zones (HIZ) in MRI images that are considered as a sign for diagnosing internal disc disruption [53], were observed posteriorly and posterolaterally (Figure 13) in people with low back pain [54,55]. MNS criterion does not appear to accurately predict failure due to the accumulation of damage under daily physiological loading conditions. In term of propagation of annular tears also Tsai-Wu seems to present reasonable results. Radial tears were observed in compression, combination of compression and flexion, and combination compression and flexion in 30° orientation (combined flexion and lateral bending). Concentric tears or delamination of the annular was not observed in the MRI images [55], whereas these are known as part of the damage during degeneration process. In all of the loading conditions, damage according to both criteria propagated in the circumferential direction due to the high shear stress [23] in the middle layers.
Several assumptions and limitations of the analysis in this study should be noted. Water content and porosity of the disc were not included in the analysis, although they can have an impact on the damage evaluation of soft tissues. However, for the duration of static loads considered in this study these effects are thought to be small. Further analysis needs to be conducted to evaluate these effects. The healing ability of in-vivo organs is also difficult to understand with current knowledge and it was not incorporated in this study. The annulus region was considered as a homogeneous material in term of fiber orientation and density. It has been shown that the orientation of fibers changes from the inner to the outer part of AF [56]. However, this assumption should not change the results obtained significantly, since different strength for different anatomical regions were considered. For more accurate analyses, it is necessary to consider this heterogeneous property of annulus. Viscoelasticity is another characteristic of soft tissues [57,58] which was not considered since the focus of this study was on damage initiation location and propagation. Finally, in this study strength of the material was considered under static loading. However, for calculating life of the tissue, although challenging, extension of the results to cyclic loading conditions is necessary.
Summary
Although a number of experimental and numerical studies over the last two decades have significantly improved our knowledge of damage in AF, consensus on a proper mechanical parameter to quantify the damage does not yet exist. In this study, Tsai-Wu and maximum normal stress (MNS) criteria were used to evaluate and quantify damage under a variety of loading conditions including compression, flexion, extension, and their combinations. The FEA results obtained in this study were compared with available experimental and clinical observations from the literature. The two damage criteria generally predicted different damage initiation locations, propagation, and distribution under the different loading conditions. MNS criterion results in a higher damage value for the great majority of the loading conditions considered. Tsai-Wu criterion predictions were in general in better agreement with the available experimental results and clinical observations. Based on both damage criteria, for the same moment magnitude a higher damage is caused in pure flexion than in pure extension, and combination of flexion and low level of compression decreases the maximum damage value compared to pure flexion. Also, higher compressive forces produce more damage than higher bending moments and increasing compression in extended FSU produces a higher damage than a flexed FSU. Based on the analysis presented, accumulation of damage under daily physiological loading conditions is at the posterior region of the disc, in accordance with the Tsai-Wu damage criterion and in agreement with MRI images in people with lower back pain. It also seems that compression plays an important role in appearance of radial tears in combined loading conditions and by applying flexion, damage is more concentrated in the posterolateral region of the AF. In all the loading conditions concentric tears are observed and explained by delaminated AF in almost all of the degenerated discs.
References
- Andersson G. B (1999) Epidemiological features of chronic low-back pain. The Lancet : 581–585
- Adams M A and Hutton W C(1982) Prolapsed intervertebral disc. A hyperflexion injury 1981 Volvo award in basic science. Spine 7: 184–191
- Osti O L, Vernon-Roberts B, Moore R, Fraser R D (1992) Annular tears and disc degeneration in the lumbar spine: A post-mortem study of 135 discs. J. Bone Joint Surg. Br. 74: 678–682
- Vernon-Roberts B, Moore R J, Fraser R D(2007) The natural history of age-related disc degeneration: The pathology and sequelae of tears. Spine 32: 2797–2804.
- Osti O L, Vernon-Roberts B, Fraser R D(1990) Volvo award in experimental studies. Anulus tears and intervertebral disc degeneration: An experimental study using an animal model. Spine 15: 762–767
- Hirsch Cand Schajowicz F (1952) Studies on structural changes in the lumbar annulus fibrosus. Acta Orthop. Scand. 22: 184–231
- Hilton R Cand Ball J(1984)Vertebral rim lesions in the dorsolumbar spine. Ann. Rheum. Dis. 43: 302–307.
- Adams M A and Hutton W C(1985) Gradual disc prolapse. Spine 10: 524–531.
- Liu Y K, Njus G, Buckwalter J, Wakano K(1983) Fatigue response of lumbar intervertebral joints under axial cyclic loading. Spine 8(8), 857–865.
- Adams M A and Hutton W C (1983) The effect of fatigue on the lumbar intervertebral disc. J. Bone Joint Surg. Br. 65: 199–203
- Callaghan J P, and McGill S M (2001) Intervertebral disc herniation: studies on a porcine model exposed to highly repetitive flexion/extension motion with compressive force. Clin. Biomech. 16: 28–37
- Gordon S J, Yang K H, MayerP J, Mace Jr A H, Kish V et al. (1991) Mechanism of disc rupture: A preliminary report. Spine 16: 450–456
- Gilbertson L G, Goel V K, Kong W,Clausen J D(1995) Finite Element Methods in Spine Biomechanics Research. Crit. Rev. Biomed. Eng. 23: 411–473.
- Goel V K, Kong W, Han J S, Weinstein J N Gilbertson L G A (1993) Combined finite element and optimization investigation of lumbar spine mechanics with and without muscles. Spine 18: 1531–1541
- Shirazi-Adl S A, Shrivastava S C, Ahmed A M(1984) Stress analysis of the lumbar disc-body unit in compression: A three-dimensional nonlinear finite element study. Spine 9: 120–134
- Li H, and Wang Z(2006) Intervertebral disc biomechanical analysis using the finite element modeling based on medical images. Off. J. Comput. Med. Imaging Soc 30:363–370
- Yao J, Turteltaub S R , Ducheyne P A (2006) Three-dimensional nonlinear finite element analysis of the mechanical behavior of tissue engineered intervertebral discs under complex loads. Biomaterials27: 377–387
- Lu Y M, Hutton W C, Gharpuray V M(1996) Do bending, twisting, and diurnal fluid changes in the disc affect the propensity to prolapse? A viscoelastic finite element model. Spine 21:2570–2579
- Shirazi-Adl A(1989) Strain in fibers of a lumbar disc. Analysis of the role of lifting in producing disc prolapse. Spine 14: 96–103
- Schmidt H, Kettler A, Heuer F, Simon U, Claes L et al.(2007) Intradiscal pressure, shear strain, and fiber strain in the intervertebral disc under combined loading. Spine 32: 748–755
- Wang J L, Parnianpour M, Shirazi-Adl A, Engin A E(1997) Failure criterion of collagen fiber: Viscoelastic behavior simulated by using load control data. Theor. Appl. Fract. Mech 27: 1–12
- Goel V K, Monroe B T, Gilbertson L G, Brinckmann P(1995) Interlaminar Shear Stresses and Laminae Separation in a Disc: Finite element analysis of the L3-L4 motion segment subjected to axial compressive loads. Spine 20:689–698
- Eberlein R, Holzapfel G A, Schulze-Bauer C A J (2001) An anisotropic model for annulus tissue and enhanced finite element analyses of intact lumbar disc bodies. Comput. Methods Biomech. Biomed. Engin 4: 209–229
- Kim Y(2000) Prediction of peripheral tears in the anulus of the intervertebral disc. Spine 25: 1771–1774
- Qasim M, Natarajan R N, An H S, Andersson G B(2012) Initiation and progression of mechanical damage in the intervertebral disc under cyclic loading using continuum damage mechanics methodology: A finite element study. J. Biomech. 45:1934–1940
- Natarajan R N, Williams J R, Lavender S A, Andersson G B (2007) Poro-elastic finite element model to predict the failure progression in a lumbar disc due to cyclic loading. Comput. Struct. 85: 1142–1151
- Dejak B, Mlotkowski A, Romanowicz M(2005) Finite element analysis of mechanism of cervical lesion formation in simulated molars during mastication and parafunction. J. Prosthet. Dent 94: 520–529
- Wolfram U, Gross T, Pahr D H, Schwiedrizik J, Wilke H J. Et al. (2012) Fabric-based Tsai–Wu yield criteria for vertebral trabecular bone in stress and strain space. J. Mech. Behav. Biomed. Mater 15: 218–228
- Shahraki M N, Fatemi A, Goel V K, Agarwal A K(2015) Effects of stress state on annulus material modeling of intervertebral disc. Frontiers in Bioengineering and Biotechnology, Section Biomechanics.
- Goel V K, Ramirez S A, Kong W, Gilbertson L G(1995) Cancellous bone Young’s modulus variation within the vertebral body of a ligamentous lumbar spine: Application of bone adaptive remodeling concepts. J. Biomech. Eng 117: 266–271
- Holzapfel G A, Gasser T C, Ogden R W (2000) A new nonstitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. Phys. Sci. Solids 61:1–48
- Gasser T C, Ogden R W, Holzapfel G A(2006) Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 3: 15–35
- Green TP, Adams M A, Dolan P(1993) Tensile properties of the annulus fibrosus. Eur. Spine J 2: 209–214
- Ebara S, Iatridis J C, Setton L A, Foster R J, Mow V C et al. (1996)Tensile properties of nondegenerate human lumbar anulus fibrosus. Spine 21: 452–461
- Fujita Y, Duncan N A, Lotz J C (1997) Radial tensile properties of the lumbar annulus fibrosus are site and degeneration dependent. J. Orthop. Res. Off. Publ. Orthop. Res. Soc 15:814–819
- Little J P (2004) Finite element modeling of anular lesions in the lumbar intervertebral disc.
- Lauren Isaacs J (2012)Micromechanics of the annulus fibrosus: Role of biomolecules in mechanical function.
- Elliott D M and Setton L A (1999) linear material model for fiber-induced anisotropy of the anulus fibrosus. J. Biomech. Eng. 122: 173–179
- Tsai S W and Wu E M(1971) A general theory of strength for anisotropic materials. J. Compos. Mater 5: 58–80
- Patwardhan A G, Havey R M, Meade K P, Lee B, Dunlap B (1999) A follower load increases the load-carrying capacity of the lumbar spine in compression. Spine 24: 1003–1009
- Nachemson A(1966) The load on lumbar disks in different positions of the body. Clin. Orthop 45: 107–122
- Panjabi M M, White A A, Brand Jr R A(1974) A note on defining body parts configurations. J. Biomech. 7(4), 385–387
- Aultman C D, Scannell J, McGill S M(2005) The direction of progressive herniation in porcine spine motion segments is influenced by the orientation of the bending axis. Clin. Biomech 20: 126–129
- Gunning, J L, Callaghan J P, McGill S M(2001) Spinal posture and prior loading history modulate compressive strength and type of failure in the spine: A biomechanical study using a porcine cervical spine model. Clin. Biomech 16: 471–480
- Qasim M (2012) Initiation and progression of lumbar disc degeneration under cyclic loading: A finite element study.
- Gasser T C, Schulze-Bauer C A, Holzapfel G A (2002) three-dimensional finite element model for arterial clamping. J. Biomech. Eng 124: 355–363
- Natarajan R N, Ke J H, Andersson G B(1994) A model to study the disc degeneration process. Spine 19: 259–264
- Krag M H, Seroussi R E, Wilder D G, Pope M H (1987) Internal displacement distribution from in vitro loading of human thoracic and lumbar spinal motion segments: Experimental results and theoretical predictions. Spine 12: 1001–1007
- McGill S M(1997) The biomechanics of low back injury: Implications on current practice in industry and the clinic. J. Biomech. 30: 465–475
- Adams M A, McNally D S, Chinn H, and Dolan P(1994) The clinical biomechanics award paper 1993 posture and the compressive strength of the lumbar spine. Clin. Biomech 9:5–14
- Natarajan R N, Lavender S A, An H A , Andersson G B (2008) Biomechanical response of a lumbar intervertebral disc to manual lifting activities: A poroelastic finite element model study. Spine 33: 1958–1965
- Fathallah F A, Marras W S, Parnianpour M(1998) The role of complex, simultaneous trunk motions in the risk of occupation-related low back disorders. Spine 23: 1035–1042
- Park K W, Song K S, Chung J Y, Choi J M, Lee J H et al.(2007) High-intensity zone on L-spine MRI: Clinical relevance and association with trauma history. Asian Spine J 1: 38–42
- Milette P C(2000) Classification, diagnostic imaging, and imaging characterization of a lumbar herniated disk. Radiol. Clin. North Am 38: 1267–1292
- Munter F M, Wasserman B A, Wu H M, Yousem D M(2002) Serial MR imaging of annular tears in lumbar intervertebral disks. Am. J. Neuroradiol. 23: 1105–1109
- Cassidy J J, Hiltner A, Baer E (1989) Hierarchical structure of the intervertebral disc. Connect. Tissue Res 23: 75–88
- Leahy J C and Hukins D W(2001) Viscoelastic properties of the nucleus pulposus of the intervertebral disk in compression. J. Mater. Sci. Mater. Med 12: 689–692
- Keller T S, Spengler D M, Hansson T H(1987) Mechanical behavior of the human lumbar spine. I: Creep analysis during static compressive loading. J. Orthop. Res. Off. Publ. Orthop. Res. Soc 5:467–478
- Tsai K H, Lin R M, Chang G L(1998) Rate-related fatigue injury of vertebral disc under axial cyclic loading in a porcine body-disc-body unit. Clin. Biomech 13: 32–39
Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences